又是一篇没人写的算法,这门课没得参考就很尴尬
是一种分布式环境下的因果序保证算法
Pre: 消息通道,因果序
因果序是什么
一个消息通道保证因果序,意味着当两个消息的发送有依赖关系时,接收也要有依赖的关系,即:逻辑先发的一定会在逻辑上先收到。
数学一点,是这样的:
对任意两个发向同一进程的消息 $m{ij}$ 和 $m{kj}$ ,假设 $Send(m{ij})\rightarrow Send(m{kj})$ ,则 $Recv(m{ij})\rightarrow Recv(m{kj})$ ;
也就是说,发送是有逻辑依赖的关系,在接收时也是按照逻辑依赖的顺序接收的。
除了因果序,消息通道还有以下的顺序
FIFO模型:信道运行为一个先进先出的队列模型
非FIFO模型:信道为一个集合,发送者向里面添加消息,接受者在里面移除消息,添加和移除是无序的
因果序应用:三副本机制
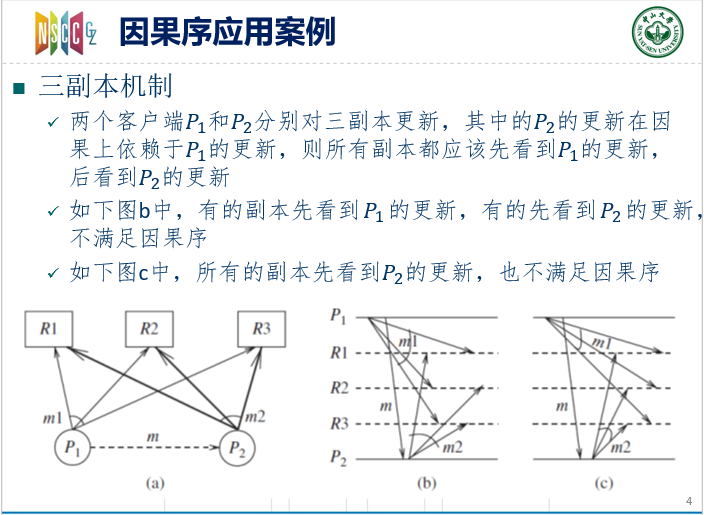
不再罗嗦了,课件非常清晰
保证因果序的基本思路
基本思路很简单
- 每条消息M都携带一条日志,保存了所有因果关系上在M之前的消息;
- M到达目的地是,先缓存自己,然后检查自己日志里的消息是否都到达了这个目的地(只检查目的地也是这里的就可以了);
- 如果满足这个要求,那么就可以把自己交付给这个目的进程了;否则要进入等待的状态;
这里有一点小问题,如果记录因果上先于M的消息呢?
很简单,如果m2依赖于m1,m3依赖于m2。那么m2携带的日志里有m1;而m3只需要复制m2的日志,再加入m2就可以了。
也就是说,将所有已发送的消息沿着因果路径不断转发就可以了。
Raynal-Schiper-Toueg算法
注意:这个算法要求FIFO通道
算法思想
基本思路是对我们上面所说的进行了简化,上面的描述中,记录了所有的消息,带来了很大的冗余。
我们考虑在FIFO通道下。当m2收到时,m1一定也已经收到了。进一步思考,发送者要求这条消息依赖于之前的,i->j的10条消息,如果j进程发现自己当前已经收到了来自i的20条消息,那么可以肯定,要求的那10条消息肯定包含在我们已收到的20条消息里(FIFO的特性,i->j通道上不会出现乱序)。
也就是说,我们只需要记录我们依赖的通道上的消息数量就可以了,这样就简化了传递的消息复杂度。
算法详述
算法详细描述如下:

Send[j,k]记录本进程所知的进程j发送到进程k的消息数量DELIV[j]记录由进程j发来的、已经Deliver到本进程的消息数
发送消息时:
i->j发送消息,表明所有依赖的消息是自己当前的SENT矩阵,附带在消息里发送,然后SENT[i, j]++;
接受消息时:
j->i发送消息,接收到j的ST矩阵,就是当前消息的依赖,我们判断我们收到的消息数量(x是每个进程编号)
满足时,确认已收到了所有依赖的消息
然后对SENT按位取max,自身和当前消息的依赖都要满足;
然后DELIV[j]++,这是接收到的来自j的消息数量;

