光栅化算法,主要是:
- DDA 画直线算法;
- Bresenham 快速画直线算法;
- Bresenham 画圆算法;
- Edge Equation 三角形填充算法;
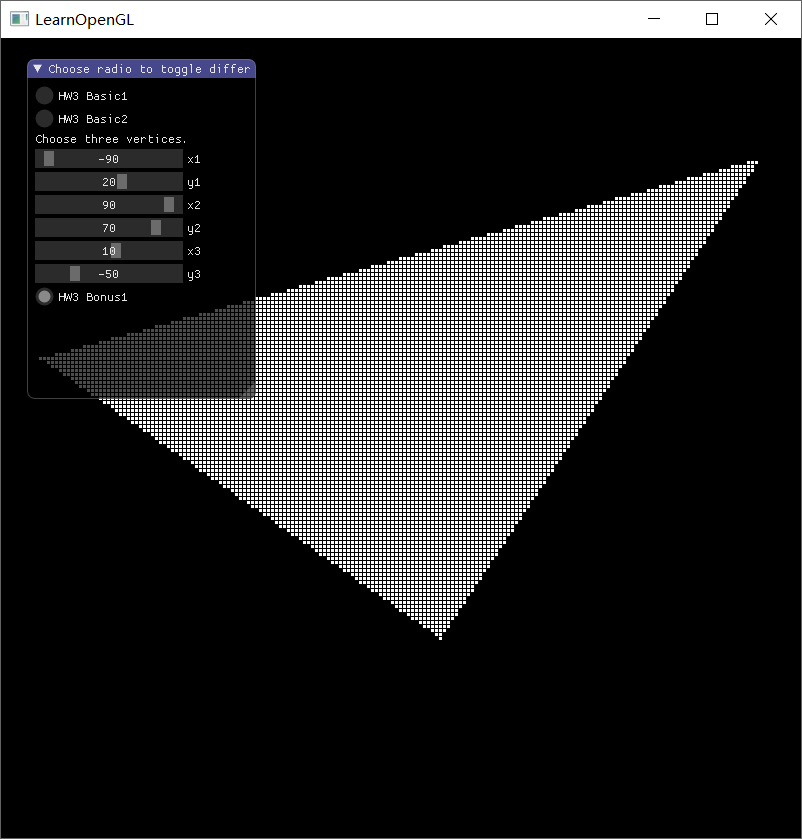
实现结果
先看效果啦,分别是使用Bresenham算法画直线、圆、并使用Edge Equation算法填充三角形的效果
DDA
想了想还是先提一句DDA吧,这个也是经典了
DDA就是简单的数值微分然后拟合的算法,它的原型大致过程如下:
- 给两个点 $(x_1, y_1),(x_2, y_2)$
- 可以得到一个直线的表达式 $y=mx+b$
- 每次推进一个$x$,即每次 $x=x+1$,然后计算 $y=mx+b$ 的值,每次要进行取整;
如果 $m>1$,那么可以选择每次将 $y$ 推进1格。
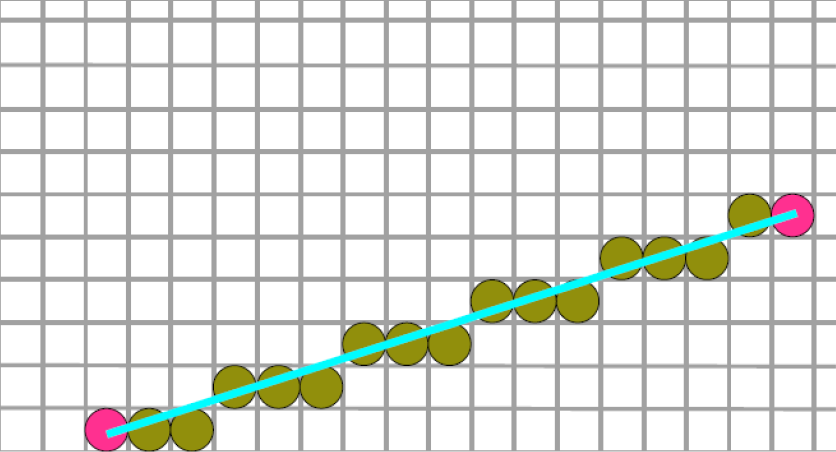
通常来说,DDA对上述过程做了一定的优化,每次不需要都计算 $y=mx+b$ 了,而是选择如下的公式计算:
到了 $m>1$ 时就换成 $x_{k+1}=x_k+\frac{1}{m}$ 就好了,计算出结果以后取整作为像素点的坐标值。
看起来好了很多,但是还是要涉及到浮点数的运算,还有不少的取整操作,对于计算机来说实在是有点困难(因为会算的很多,浮点总是要慢一些的,还会涉及到一定的舍入误差累计)。
Bresenham算法
感谢Bresenham老爷子提出的这个Bresenham算法,现在这基本上是所有直线算法的标准了,一般都会直接集成到硬件里。
Bresenham 直线算法原理
先上一张图
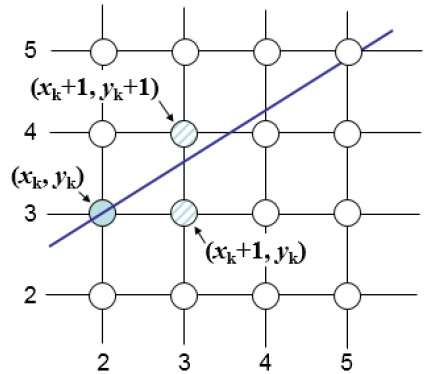
可以看出来,每次选下一个点都是在 $(x_k+1, y_k+1)$ 和 $(x_k + 1, y_k)$ 之间选取,到底选哪个要看直线到底在这个x坐标下,离哪个更近一些。
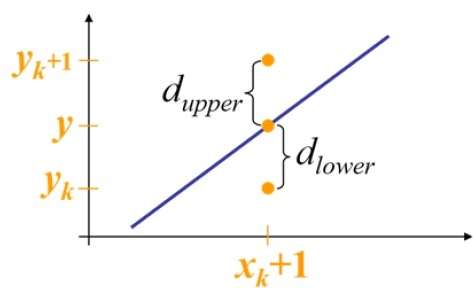
我们把上下的距离分别标注为 $ d{upper} $ 和 $d{lower}$ ,当下边比较大的时候,就要选取上边的点,所以我们让他们相减,代入直线公式可以得到
我们已经知道了 $\Delta x = x{end} - x{start} $ 是一个正值,所以我们可以把这个乘到上式,不会影响正负。
这里 $\Delta x= x{end} - x{start}, \Delta y = y{end} - y{start},m=\Delta y/ \Delta x$
$c=(2B-1)\Delta x + 2 \Delta y$;
然后我们可以代入算出来
第二步代入了直线方程
要注意这个公式只有 $p_0$ 可以这样推导出来,因为 $\overline {y_0} = mx_0 + B$,而其他的 $y_i$ 就不能这么简单的算出来了。
$\overline{y_i}$ 就是在 $i$ 这个点处,光栅化以后的纵坐标的值
还可以进一步的化简
这里如果 $pi \leq 0$,那么 $\overline {y{i+1}} - \overline{yi} = 0$,那么 $p{i+1} = p_{i} + 2 \Delta y$;
这里如果 $pi > 0$,那么 $\overline {y{i+1}} - \overline{yi} = 1$,那么 $p{i+1} = p_{i} + 2 \Delta y - 2 \Delta x$;
简直是神器啊,得到这个以后就可以开始计算了,全是整数,不浮点不取整不舍入,还是拟合效果最棒的,贴一张图看个例子:
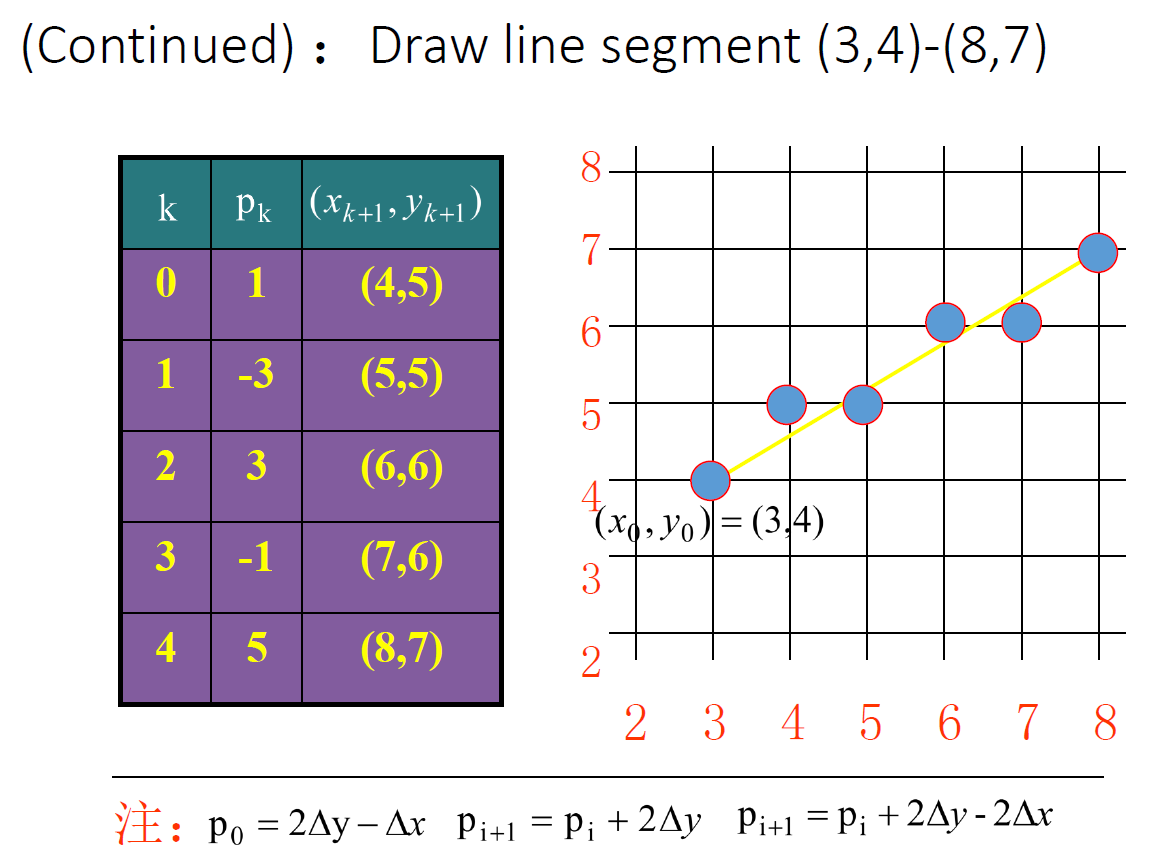
Bresenham 直线算法实现
这里使用了几个标志量:flipY和flipXY,表示我们我们对输入数据做的不同的预处理,目的都是把输入的直线转换为一个简单的形式,可以直接应用x=x+1, y=...这样的规则。
其中:
首先判断起始点的
x坐标要在终点的x坐标前,如果不符合,则交换两个点的坐标;flipY:应用的情况如下图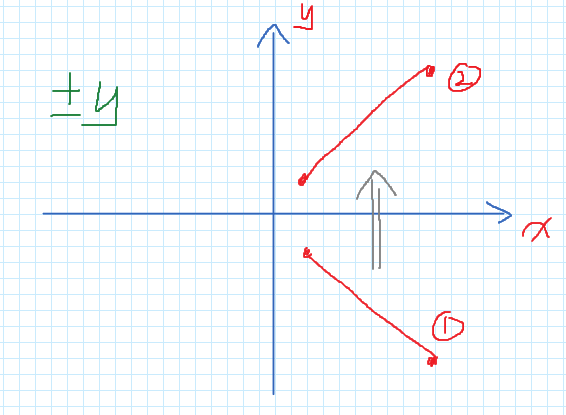
目的是将左上到右下的直线转换为左下到右上,就可以使用我们讨论的方法了;
flipXY:应用的情况如下图: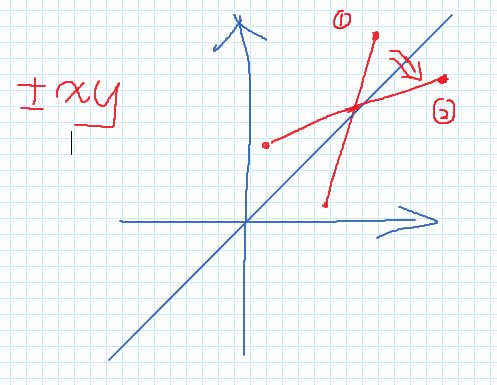
此时将纵坐标跨度较长的直线转换为了横坐标跨度较长的直线,也就可以应用我们讨论的办法了;
流程结束后,将得到的直线坐标根据这两个flag进行变换,得到真正的坐标。
代码
1 | // 生成线 |
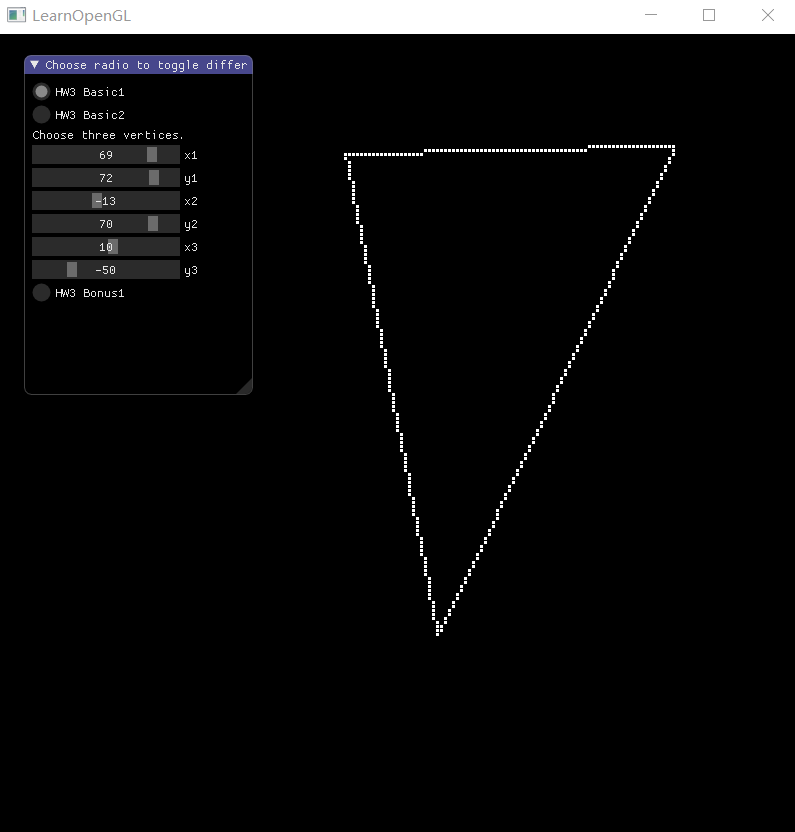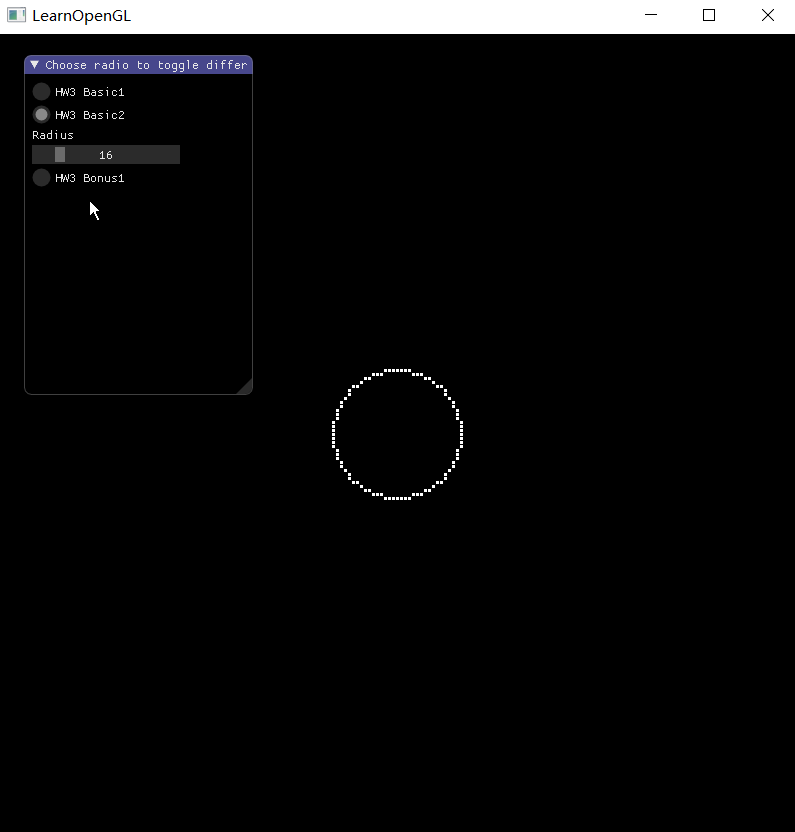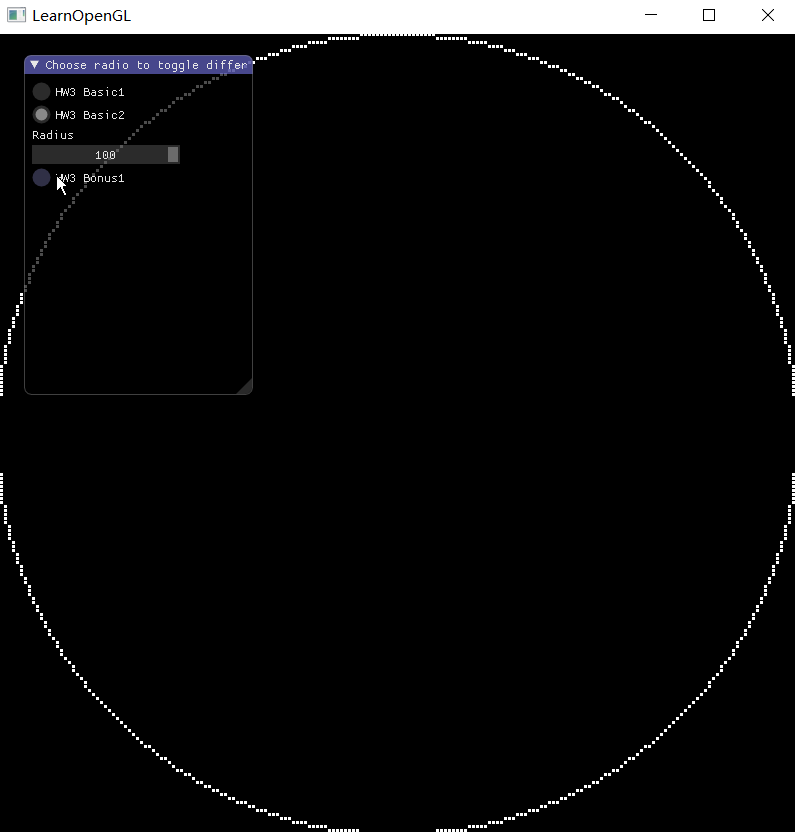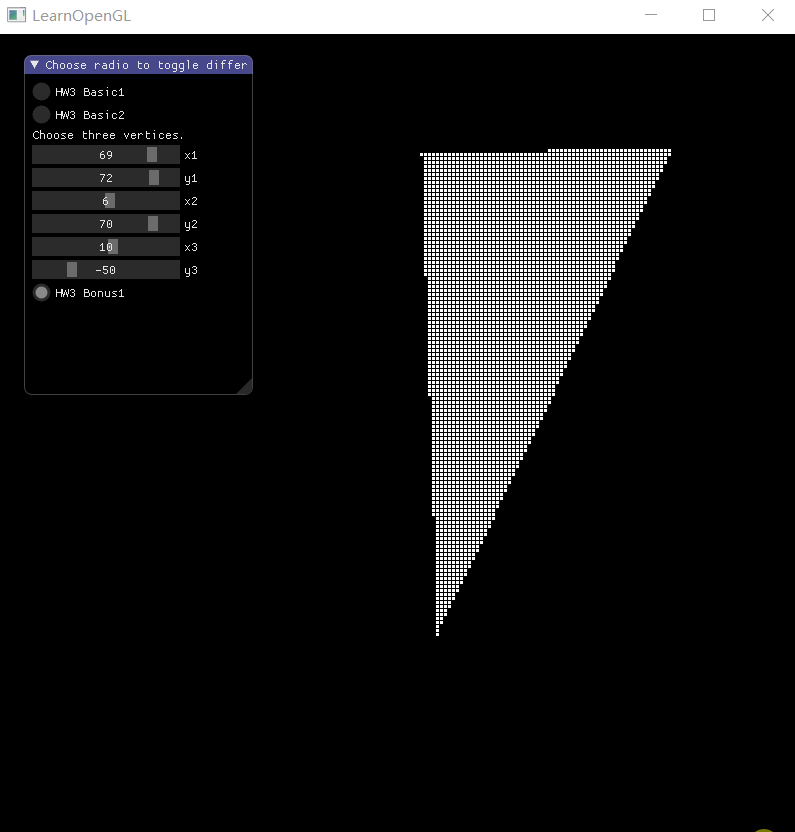
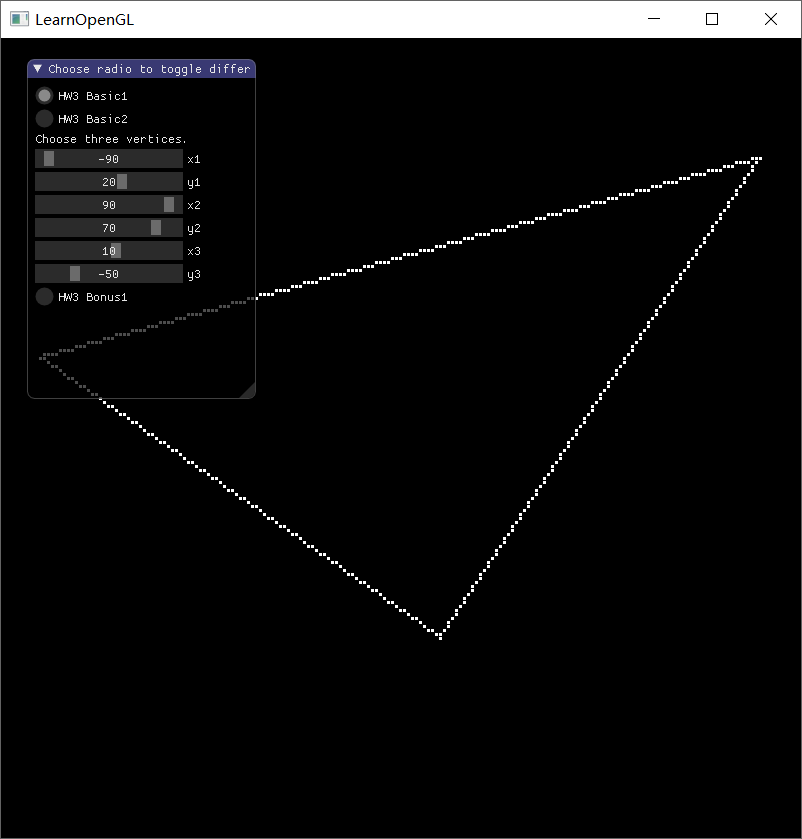
Bresenham 算法绘制三角形
就是使用 Bresenham 算法画三条线,结果如下:
Bresenham 算法画圆
算法原理概述
画圆和画直线的思路差不多,具体可以看https://en.wikipedia.org/wiki/Midpoint_circle_algorithm
同时要注意只需要画1/8圆就可以了,其他的部分可以对称过去。
起始的 $d = 3 - (2 * r)$,每次 $x = x + 1$,计算 $d$ 而得到 $y$ 坐标的值。
算法流程如下: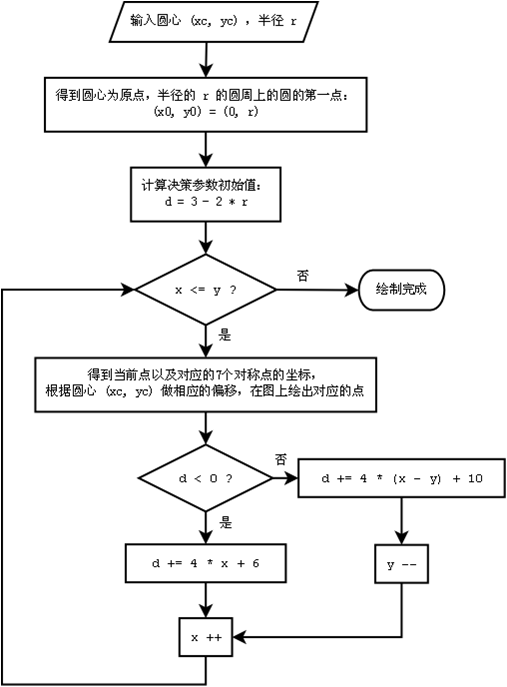
代码实现
1 | // 生成圆 |
实验结果
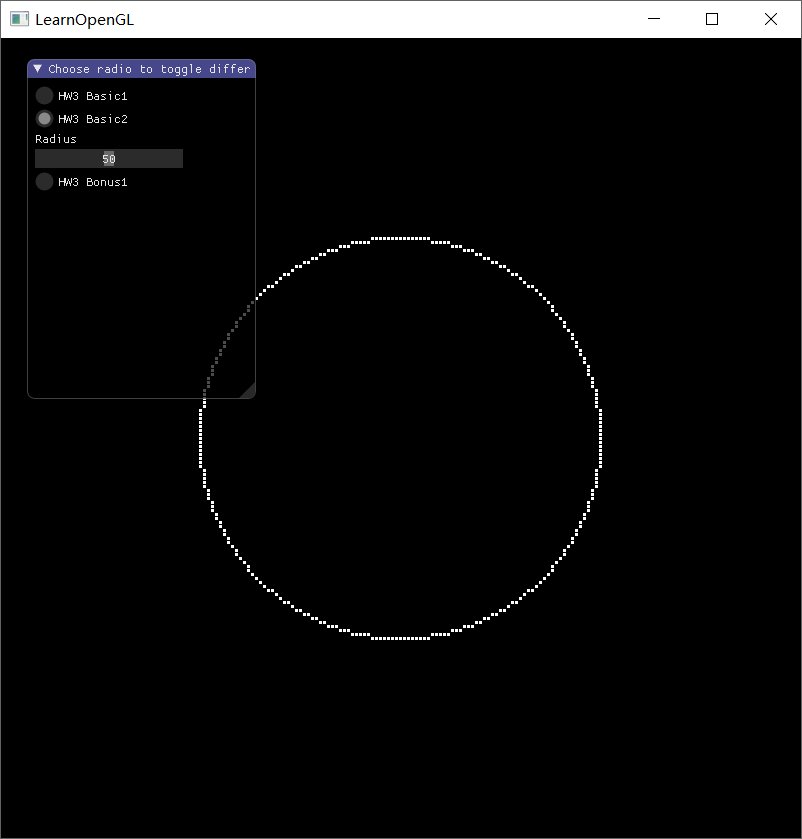
Edge Equation 三角形填充算法
Edge Equation 算法原理概述
三角形的填充使用Edge Equation算法,具体实现流程如下:
计算得到一个矩形框,如下图黄色部分,将三角形全部包括进去;
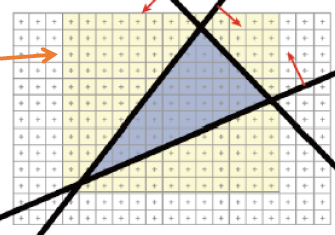
对矩形框内每个点进行计算,判断其是否在三角形的内部,如果在内部则进行渲染,否则不进行渲染;
这一步使用的是简单的直线方程进行计算,首先我们可以得到两点的直线方程为:
对每个点应用该公式,判断其正负性,则可以判断是否在三角形内部;
具体使用时可能难以判断其正负性那个是在内部,可以使用第三个点辅助判断,与第三个点带入方程的符号相一致的是在三角内部的点,否则是在三角外部的点;
伪代码如下:

Edge Equation算法实现
1 | std::function<bool(int x, int y)> genLineEquation(Point p1, Point p2, Point p3) { |
实验结果