Linear Regression
Assume the model is:
We can write a base class using this formula for our linear regression implement below,
1 | class LinearRegressionBase: |
And we can generate some data for test,
1 | n = 100 |
The code above represents the ground truth is
Ordinary Explicit Solution
Using Mean Square Error as the loss function
Find the derivative of $\beta$.
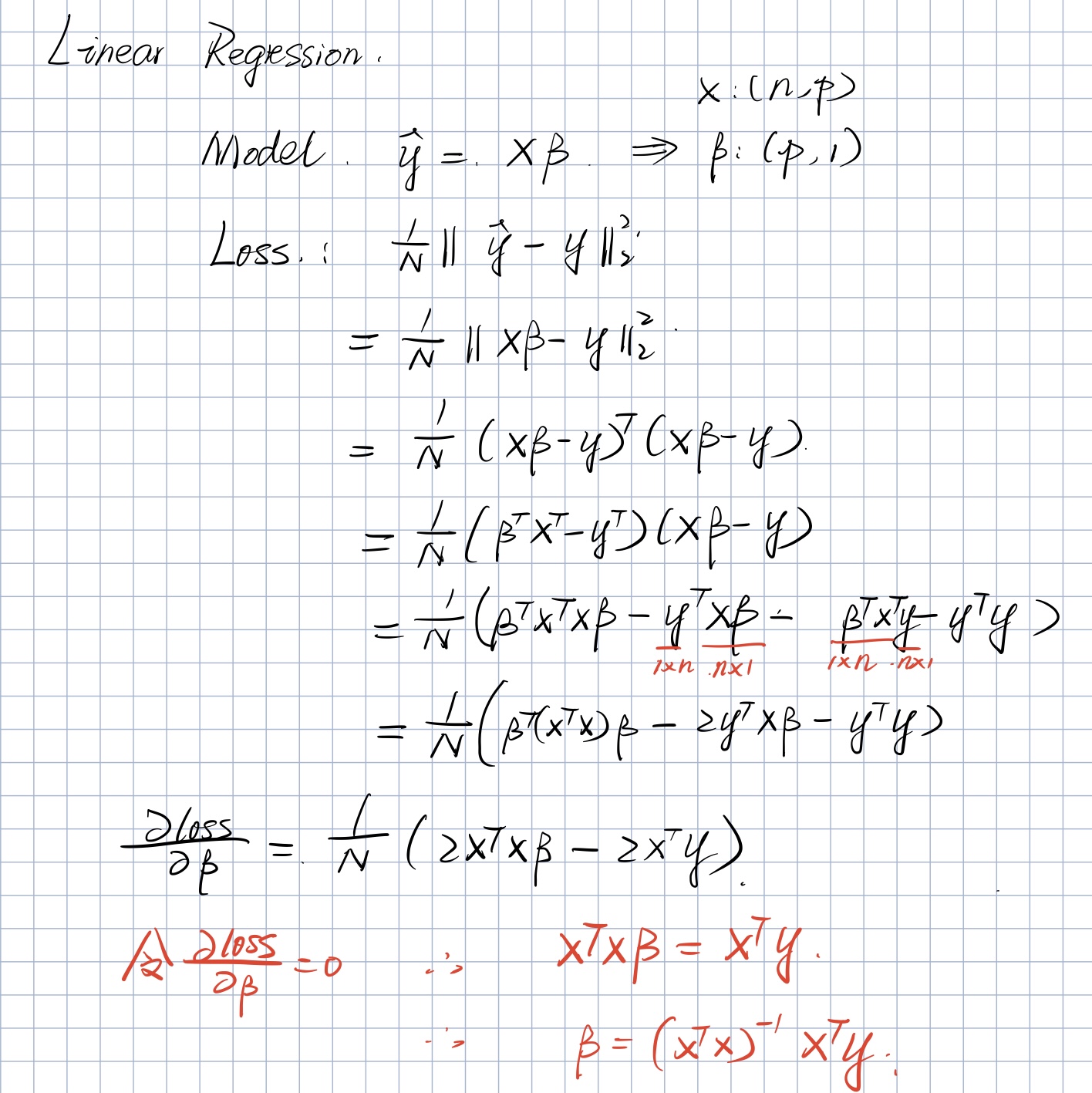
The least square solution would be like
Using python to implement that,
1 | class LinearRegression: |
And test it,
1 | lr = LinearRegressionO() |
Ridge Regression
Same as last part. But we add a l2 regularization to the loss function.
Very similar to the last part, take the derivative of $\beta$, we get
Let the derivative to be 0. We get,
We don’t need to assume the invertibility since the $(X^TX+\lambda I)$ is always invertible.
Simple proof:
Any vector is the eigenvector of $\lambda I$ since $\lambda I v = \lambda v$. And all eigenvalues of $\lambda I$ is $\lambda$.
$X^TX$ is a symmetric matrix and it’s positive semi-definite, so all the eigenvalues are bigger or equal to 0.
So any eigenvalues and eigenvectors of $X^TX$, note by $a_i, v_i$,
So all the eigenvalues of $(X^TX+\lambda I)$ is bigger or equal to $\lambda>0$.
Which means $(X^TX+\lambda I)$ is always invertible.
Using python to implement that,
1 | class RidgeRegression(LinearRegressionBase): |
And test it, using different $\lambda$,
1 | l = 10: |

